What are Modes in Diffusion Models?

Diffusion models have emerged as a powerful tool in machine learning, particularly for their ability to generate high-quality samples. While their iterative noise-to-data process resembles gradient descent at inference, there’s one key feature that makes them especially valuable for robotics: their ability to learn and generate samples from different modes in the data distribution. In this post, I’ll explain what these modes are, why they matter, and how diffusion models handle them.

But what are modes?

Assume that your data has multiple distinct patterns or clusters. For example, if you’re working with images of different types of objects, each type might represent a different mode. In robotics, at a high level this could translate to various modes of operation, such as walking, running, or climbing for a legged robot or at a low level this could translate to different ways of picking object, different turns you could take to reach the same goal position.

In statistical terms, a mode is a peak in the probability distribution of your data. In simpler terms, it’s a pattern or behavior that is commonly found in your dataset.

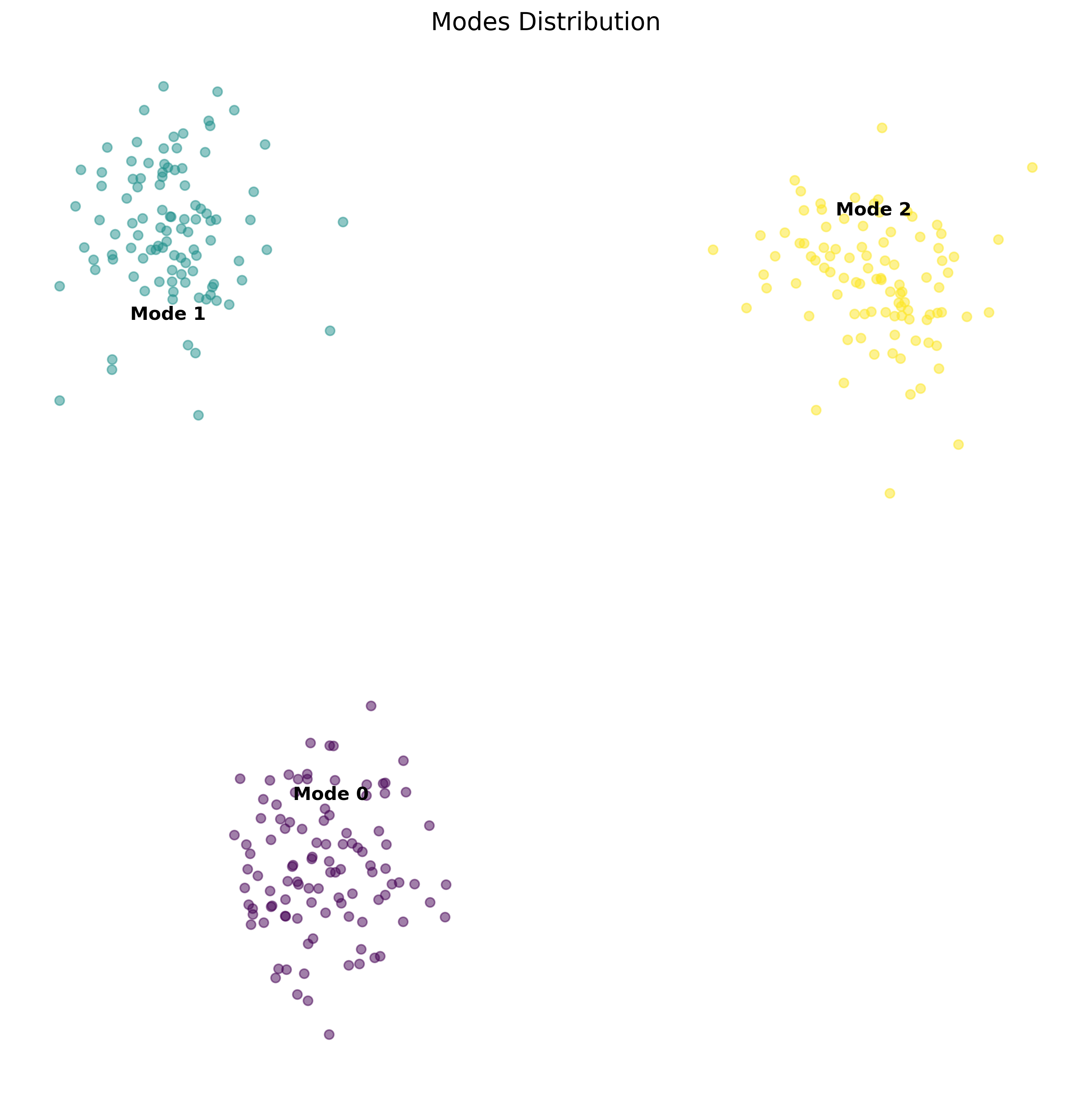
Mode Collapse

Mode collapse occurs when a model fails to capture the full diversity of the data distribution, instead converging to a single mode or a subset of modes while ignoring others. This is particularly problematic in real-world applications where capturing the full range of possible solutions is crucial.

For example, assume that your data has two modes. And you are naively trying to fit it through a simple-regression model then you might end-up with a solution whose empirical risk might be minimum but when you sample from this distribution, you will be out of distribution. This is one example of mode-collapse.

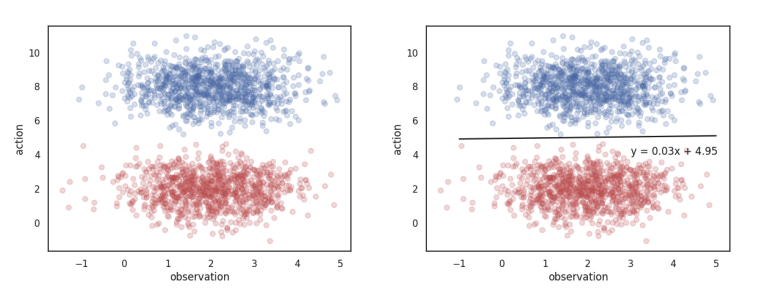
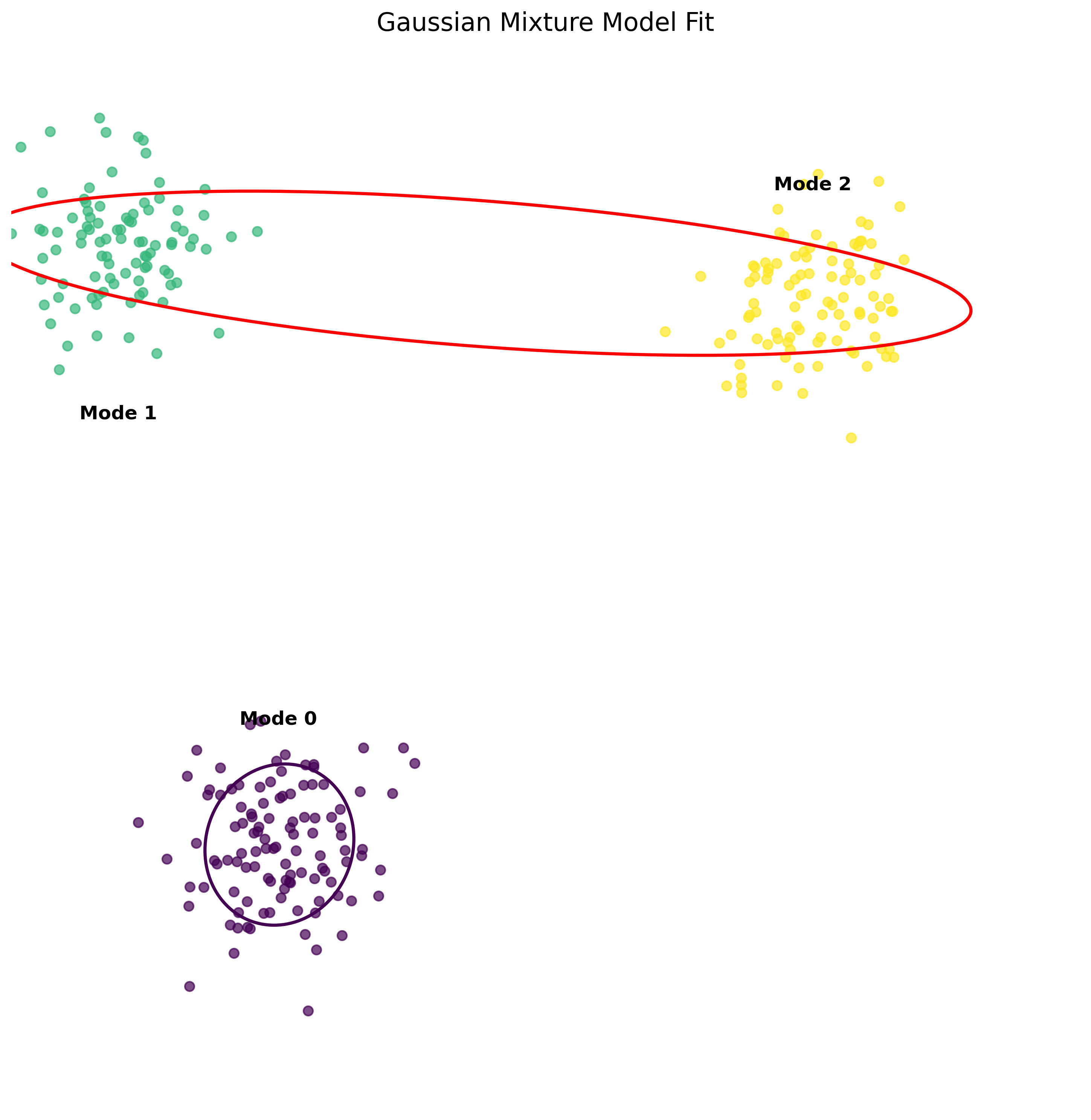
Mode Collapse in Gaussian Mixture Models (GMMs) Well, the concept of mode collapse is nothing new, it is well known and one of the famous solution for this is Gaussian Mixture Models which we have known since 1950s. However, model collape occurs in GMMs also! This happens when multiple true modes in the data are merged into a single Gaussian component. This is because the model tries to fit the data into a predefined number of Gaussians (a hyperparameter that we need to specify), which may not match the true number of modes.

Modes in Diffusion Models

I already assume that you know a little bit theory about Diffusion Models, but you can learn about them here. Diffusion models model the distribution by learning a sequence of noise-adding steps and then reversing this process to generate samples.

But why doesn’t mode collapse occur in Diffusion Models (compared to other methods)? The iterative noise-addition and reversing process (also called iterative denoising step) in diffusion act as an implicit regularization term which prevent the model from overfitting to specific training examples. This iterative denoising procedure also helps in learning multiple scales in data, where early steps focus on large broad structures or mean of the distribution and later steps focus on refining details.

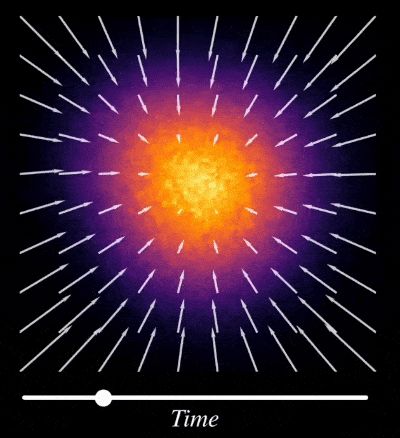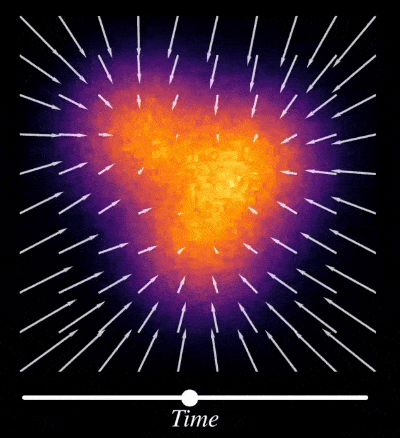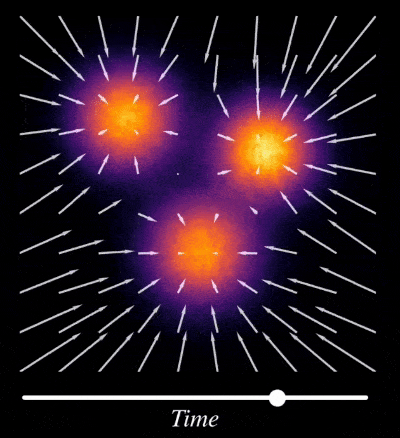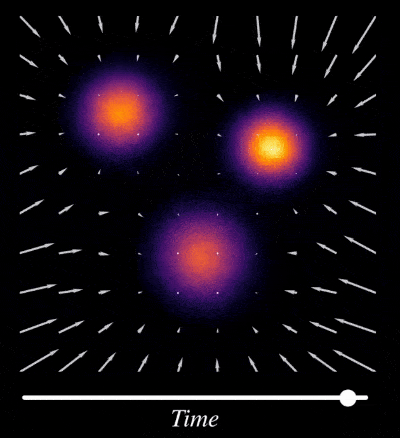
For example in image dataset multiple scales could be different levels of abstractions in the image, such as overall composition, significant textures, fine-grained details. And in robotics this could mean high-level plan to move from one point to another or low-level manipulation skills requiring precise movements.

Well probability modeling has been around for a long time, and the theory behind diffusion has also been known for a long time. But what has really changed is we have gotten really good at training large neural networks on dataset, that is the main difference between what was known vs what has recently been done. Neural networks with all the ingridients to remove obstacles in their learning have paved way to efficiently learn these modes in distributions.

Another main reason why diffusion models are able to capture and generate multiple modes in the distribution is stochastic initialization and stochastic sampling procedure. During the sampling procedure, the sample is initialized as a random sample from Gaussian Distribution this ensures that all the possible modes are covered, and the sample is stochastically optimized (which means that a small random noise is added at each timestep, this is a bit exaggerated in the below videos but it shows the point) over large number of iterations, which helps it hop over and converge to different modes.

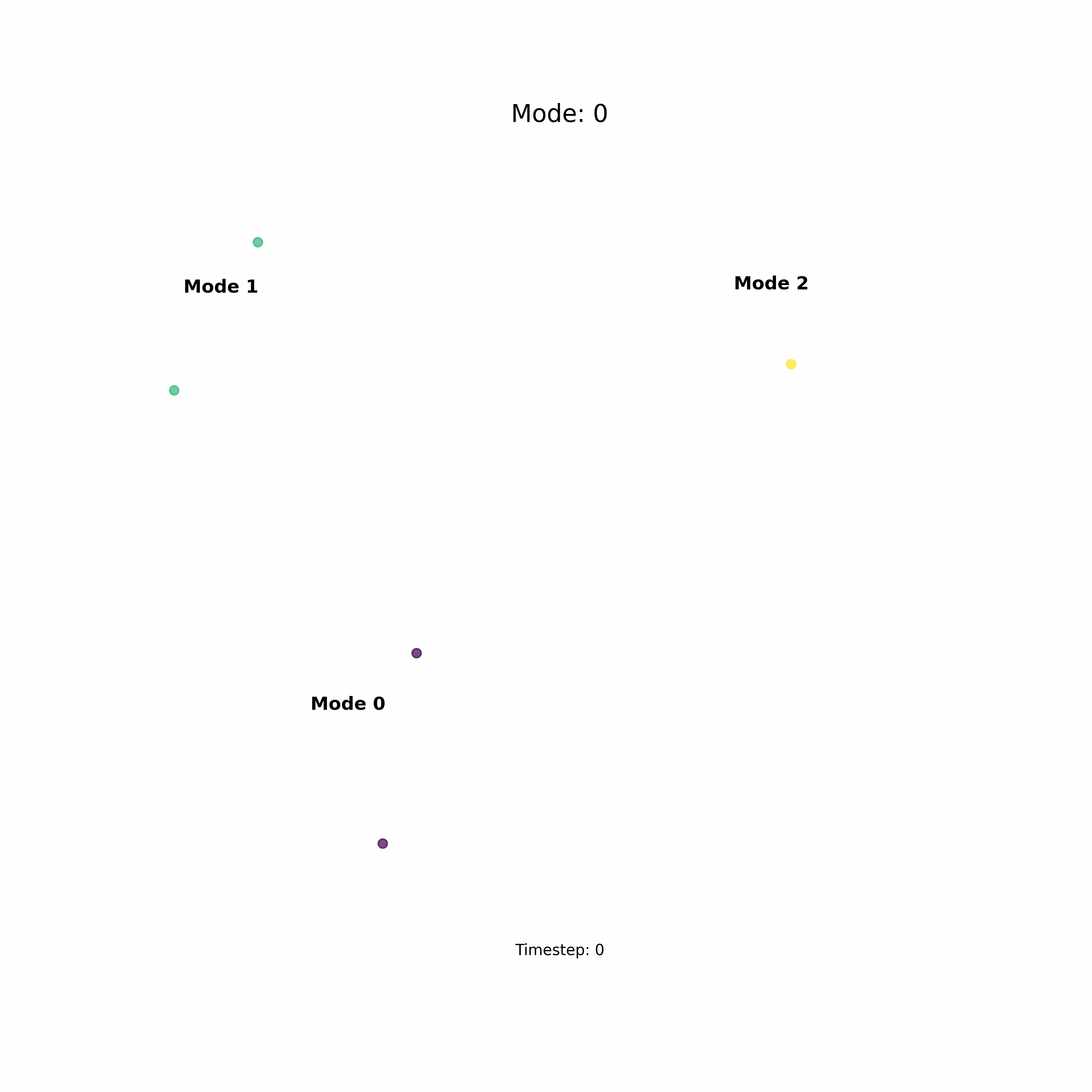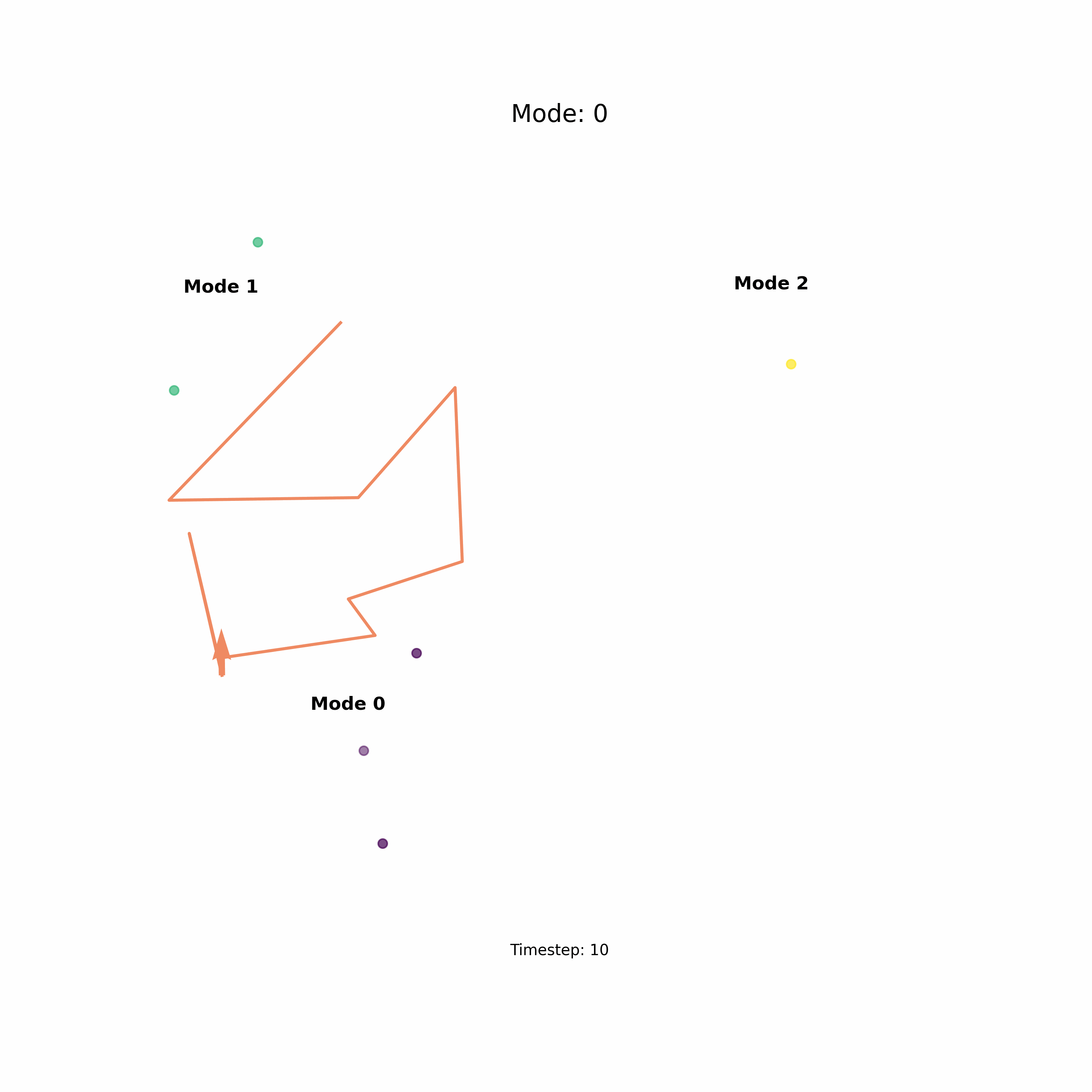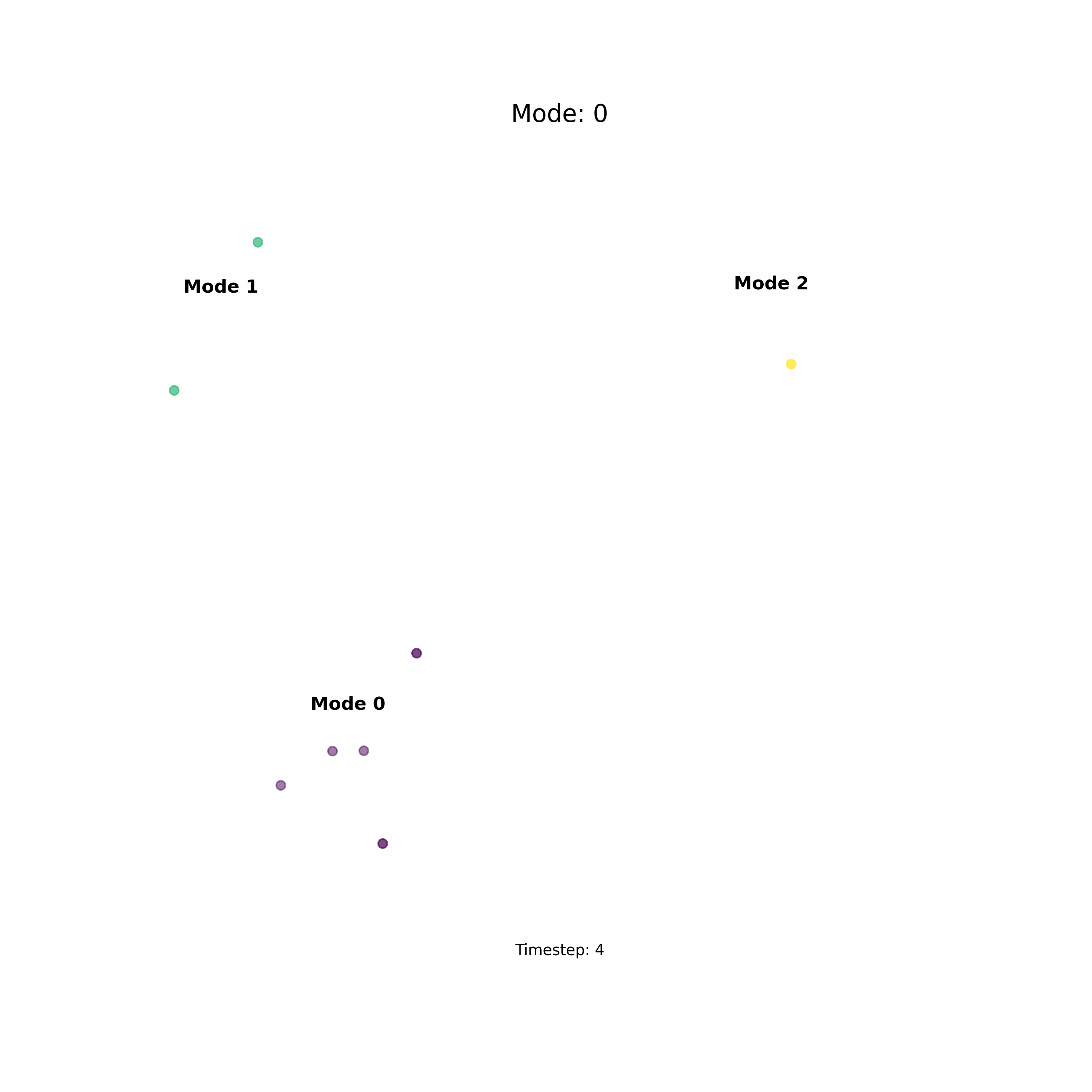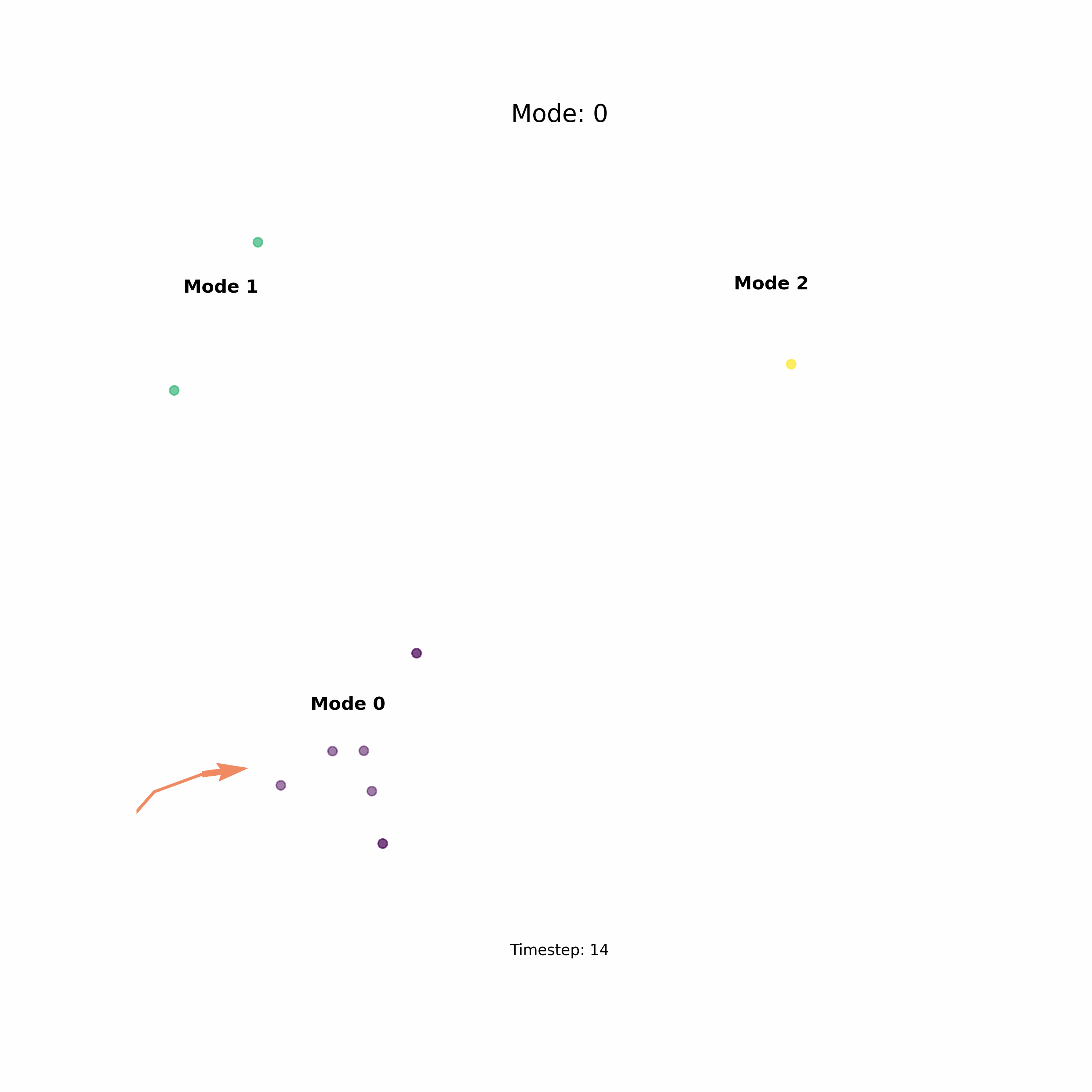
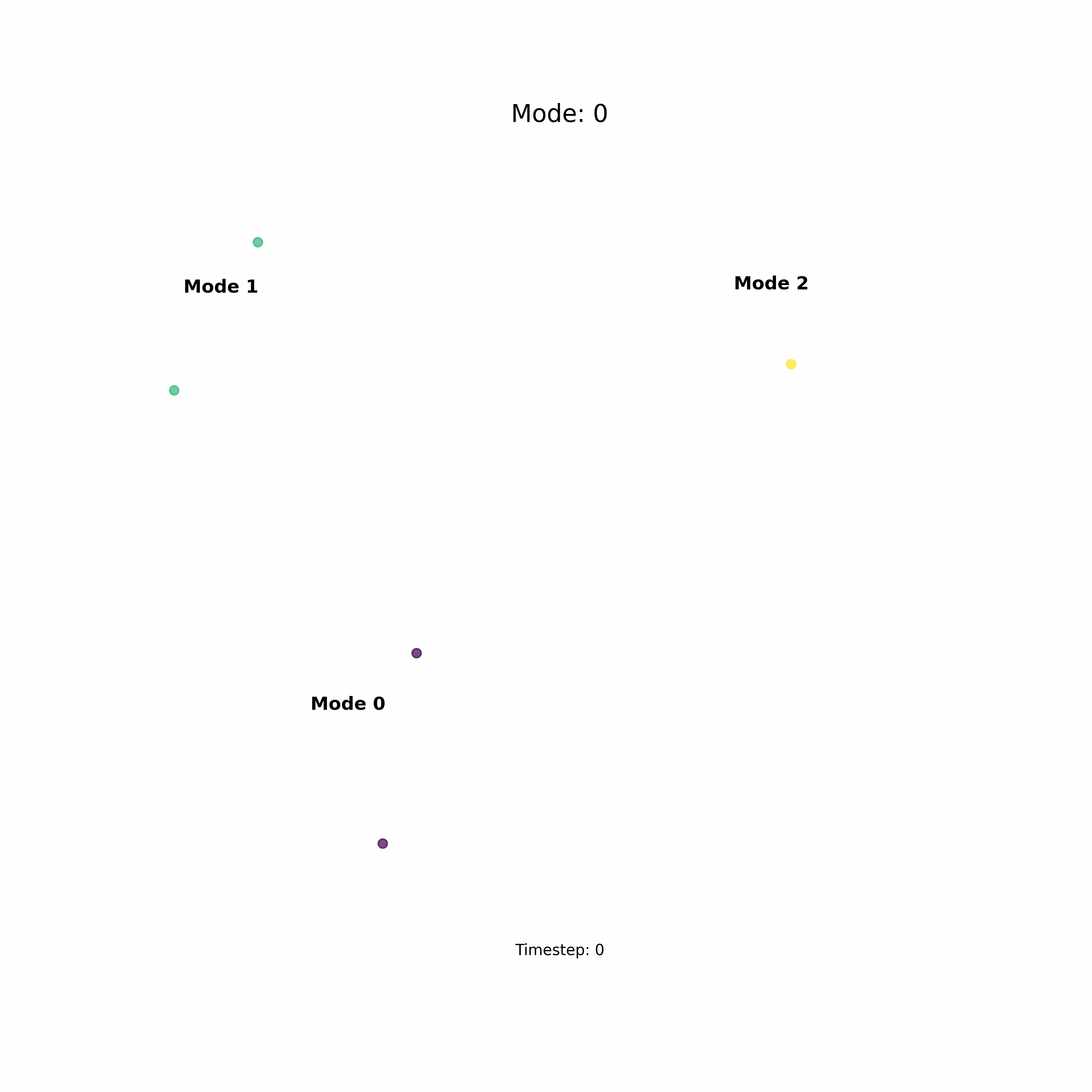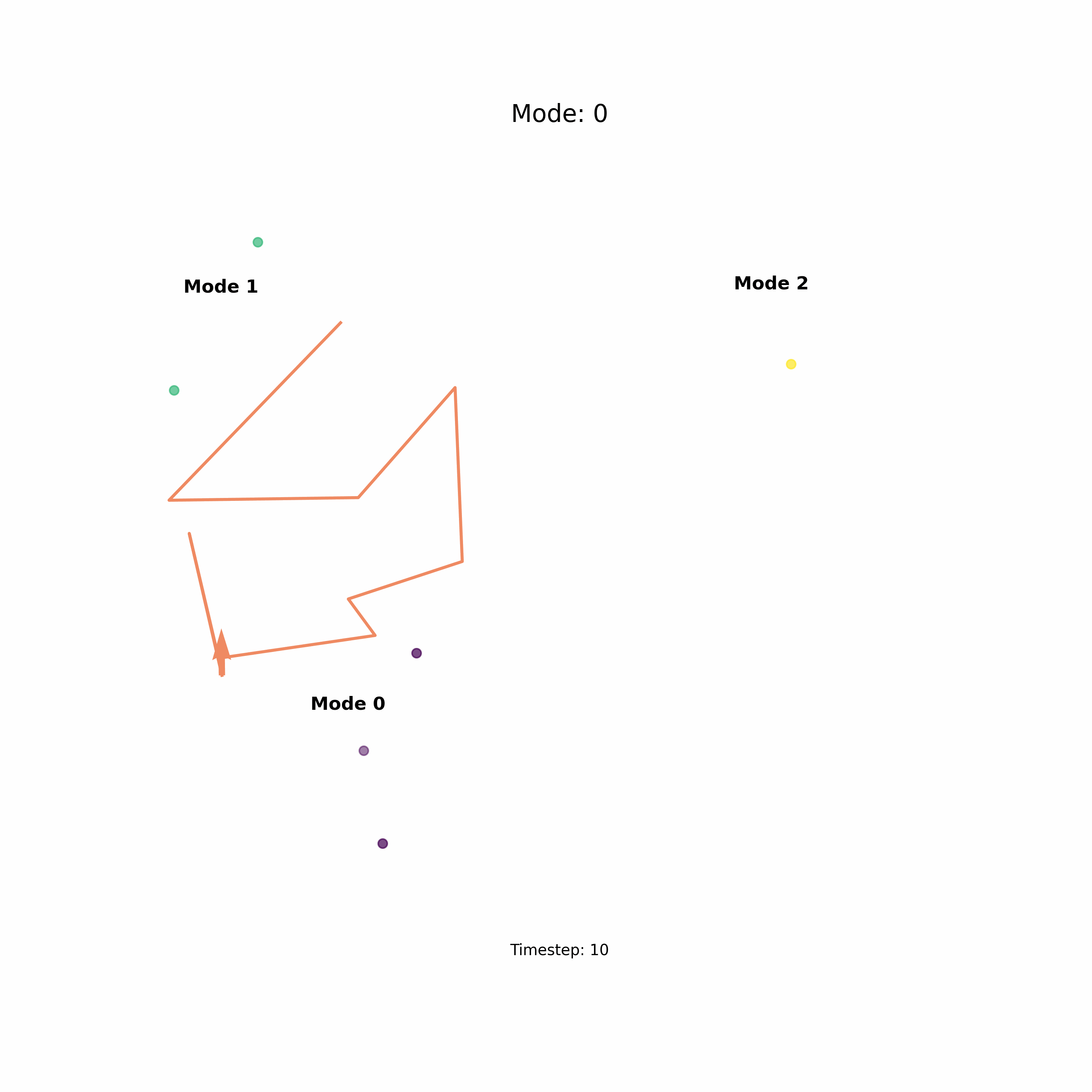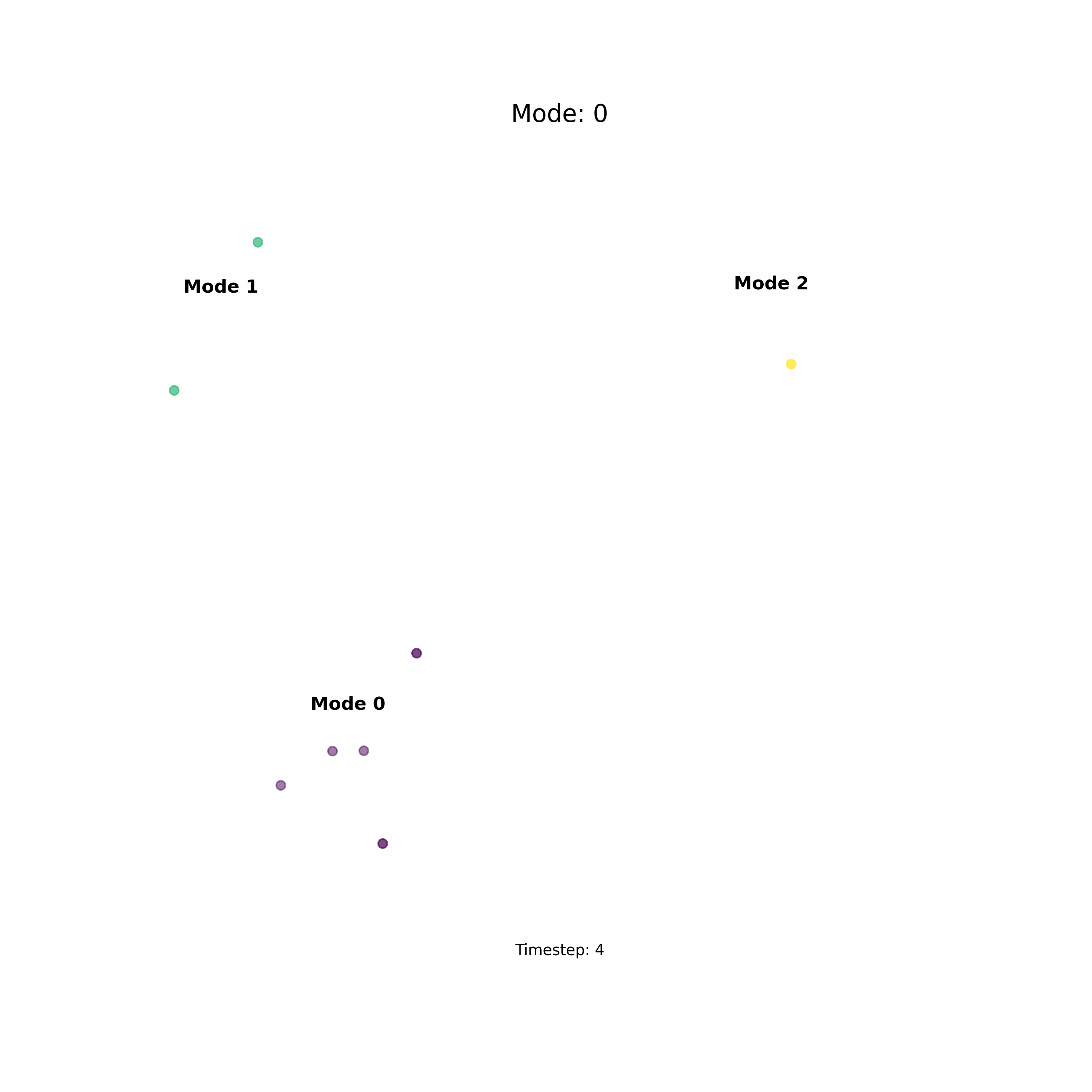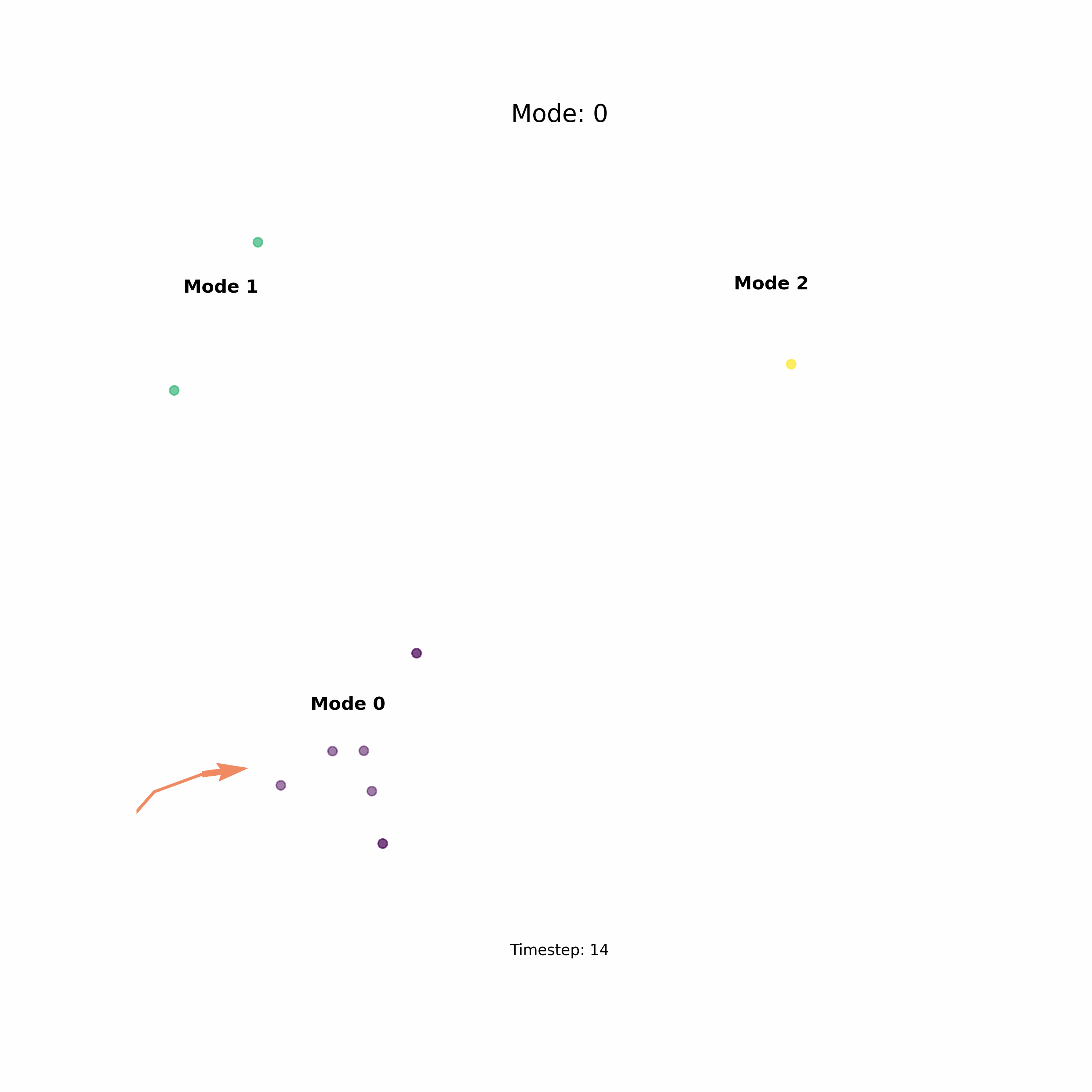
Another great advantage of diffusion models is that they render themselves to conditional generation, i.e., we can condition the generation process on some input that directs the mode of convergence. That is really cool, not only can we get sample but we can get the sample we want based on high-level conditional data. And the icing on top of the cake is that the conditioning of diffusion models is also flexible, which means we can condition the generation of sample either using a number or a language prompt or an image. This is especially useful in robotics where you want to convert control your robots action or policy using high-level natural language commands. Here in the below example, I sample a data point from the distribution based on numerical specification of the mode.

No Free Lunch, here too!

While diffusion models offer impressive capabilities in capturing multiple modes, they aren’t without their limitations. One particularly interesting challenge emerges when dealing with closely spaced modes. Look at the below figure, if we have means a bit closer than they are, diffusion model produces samples that are in-between the two modes (mode interpolation). This might be the reason for hallucinations that you see in most of the diffusion models outputs in internet.

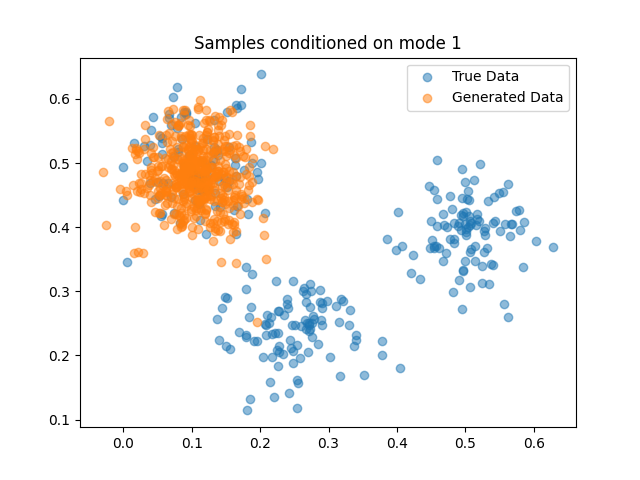
Now why this happens? As mentioned above the diffusion models learn the mean of the distribution first and then specific offsets. In frequency domain this could be termed as learning low-frequency first and then high-frequency. And neural networks particularly CNNs (which are most widely used neural network architecture for diffusion) have high affinity towards low-frequency. So they are able to model low-frequency or mean of the distribution perfectly but when it comes to high-frequency components they interpolate. This interpolation in high-frequency domain leads to mode interpolation when they are nearby. This is shown by Aithal et al. where they hypothesize that the mode interpolation might be due to inability of the neural network to mode high-frequency change in score function.

I will shamelessly plug my own paper on this topic, where we tried to solve similar issue (we had in mind the high-frequency change in value function of a RL agent) albeit for lower-dimensional input space.

Well one can solve this by training longer, but that could come at the risk of overfitting the model and reducing the diversity and also this can become increasingly infeasible as the data increases. I also hypothesize that training for longer might create a more discontinuous function which when coupled with stochastic denoising can make reliability a huge problem and might also make the models more susceptible to adversarial attacks.

Modes in Robotics

Multi-modality is very important property of robotics data. Actually almost all of the data is inherently multi-modal because there are always multiple answers for a same question unless you starting putting constraints. There might be millions of images that a generative image model might generate when you say dog, but as you put more and more constraints in your prompt the search space reduces and we get specific outputs. Same in language models, unless you are very specific the output can be unpredictable. For robotics, it means that we need our model to learn all the possible way to achieve a goal, and during inference as the constraints pop-up it changes or shifts its solution.

Consider the task above, which is an example of two dominant ways in which we can solve a problem and how it is modeled by a diffusion model.

References

“Understanding Hallucinations in Diffusion Models through Mode Interpolation” , Aithal et al.
“Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains” , Tancik et al.
“Univariate Radial Basis Function Layers: Brain-inspired Deep Neural Layers for Low-Dimensional Inputs” , Jost et al.